Top 10 Best Four Dimensional Shapes

This is the four-dimensional extension of the infamous Mobius Strip. Where the Mobius strip is a line with one boundary, a Klein Bottle is a bottle with none. Just as walking along a Mobius Strip takes you to the underside of where you started, filling a Klein Bottle causes its content to erupt from the mouth.

Just as the glome is to the sphere what the sphere is to the circle, a tesseract is to a cube what a cube is to a square. Its net consists of eight cubes. The tesseract is one of the regular 4-polytopes, or four dimensional extensions of the Platonic Solids.

A glome is a four-dimensional sphere. Just as the cross-section of a sphere is always a circle, the cross-section of a glome is a sphere.

This is a more complex uniform 4-polytope than the Platonic extensions, consisting of 320 cells; 15 tetrahedra for every pentagonal antiprism. This can be made by deconstructing the hexacosichoron, specifically by removing 20 antiprism pyramids, just as the antiprism itself can be made by disassembling an icosahedron.

Also aptly known as the 600-cell, this is the most complex extension of the simplest Platonic Solid, consisting of 600 tetrahedral cells. The dual polyhedron of the dodecacontachoron.

This is the extension of the dodecahedron into four dimensions, using 120 dodecahedral cells, and the dual polyhedron of the hexacosichoron.

Take a look at the 3D conception of one of these things rotating. It's so awesome, and could be an awesome screensaver.

The extension of the third Platonic Shape: the Octahedron, into four dimensions. Consists of 24 octahedra.

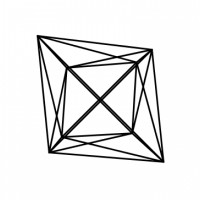
This is the dual polytope of the tesseract, and the extension of the tetrahedron, or the simplest Platonic Shape.

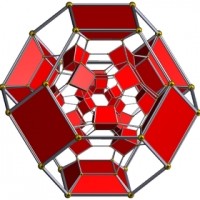
This is the truncated version of the octacube, which is the equivalent of cutting the vertices of the octacube itself. The regular octagon is the truncated square, just as this is made by cutting the cubic vertices of the octacube.